basilh@virginia.edu
@basilhalperin
Behavioral economists have a concept called loss aversion. It's almost always described something like this:
"Loss aversion implies that one who loses $100 will lose more satisfaction than another person will gain satisfaction from a $100 windfall."
– Wikipedia, as of December 2015
Sounds eminently reasonable, right? Some might say so reasonable, in fact, that it's crazy that those darn neoclassical economists don't incorporate such an obvious, fundamental fact about human nature in their models.
It is crazy – because it's not true! The pop definition of loss aversion given above – that 'losses hurt more than equivalently sized gains' – is precisely the concept of diminishing marginal utility (DMU) that is boringly standard in standard price theory.
Loss aversion is, in fact, a distinct and (perhaps) useful concept. But somewhat obnoxiously, many behavioral economists, particularly in their popular writings, have a tendency to conflate it with DMU in a way that makes the concept seem far more intuitive than it is, and in the process wrongly makes standard price theory look bad.
I'm not just cherry-picking a bad Wikipedia edit. I name names at the bottom of this post, listing where behavioral economists have (often!) given the same misleading definition. It's wrong! Loss aversion is about reference dependence.
To restate, what I'm claiming is this:
Let me walk through the difference between DMU and loss aversion painstakingly slowly:
Diminishing marginal utility
"Diminishing marginal utility" is the idea that the more you have of something, the less you get out of having a little bit more of it. For example:
If you own nothing but $1,000 and the clothes on your back, and I then give you $100,000, that is going to give you a heck of a lot more extra happiness then if you had $100 million and I gave you $100,000.
An important corollary follows immediately from this: losses hurt more than gains!
I made a super high quality illustration to depict this:
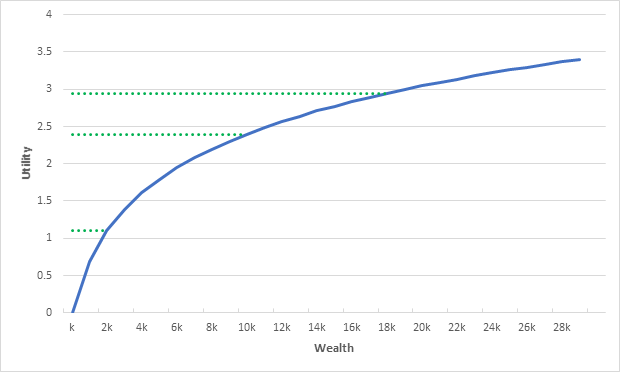
What we have here is a graph of your utility as a function of your wealth under extremely standard (i.e., non-behavioral) assumptions. The fact that the line flattens out as you get to higher wealth levels is the property of DMU.
We can also see that equivalently sized losses hurt more than gains. As you go from 10k wealth to 2k wealth (middle green line to bottom green line), your utility falls by more than the amount your utility rises if you go from 10k wealth to 18k wealth (middle green to top green lines), despite the change in wealth being the same 8k in both directions.
Standard economics will always assume DMU, thus capturing exactly the intuition of the idea described in the above Wikipedia definition of loss aversion.
More mathematically – and I'm going to breeze through this – if your utility is purely a function of your wealth, Utility=U(W), then we assume that U'(W)>0 but U''(W)<0, i.e. your utility function is concave. With these assumptions, the result that U(W+ε)-U(W) < U(W)-U(W-ε) follows from taking a Taylor expansion. See proof attached below.
Loss aversion
Loss aversion is a consequence of reference dependence and is an entirely different beast. The mathematical formulation was first made in Tversky and Kahneman (1991).
In words, loss aversion says this: Suppose you have nothing but the clothes you're wearing and $10,000 in your pocket, and then another $10,000 appears in your pocket out of nowhere. Your level of utility/happiness will now be some quantity given your wealth of $20,000.
Now consider a situation where you only own your clothes and the $30,000 in your pocket. Suppose suddenly $10,000 in your pocket disappears. Your total wealth is $20,000 – that is, exactly the same as the prior situation. Loss aversion predicts that in this situation, your level of utility will be lower than in the first situation, despite the fact that in both situations your wealth is exactly $20,000, because you lost money to get there.
Perhaps this concept of loss aversion is reasonable in some situations. It doesn't seem crazy to think that people don't like to lose things they had before.
But this concept is entirely different from the idea that 'people dislike losses more than they like gains' which some sloppy behavioral economists go around blathering about. It's about reference dependence! Your utility depends on your reference point: did you start with higher or lower wealth than you currently have?
In their academic papers, behavioral economists are very clear on the distinction. The use of math in formal economic models imposes precision. But when writing for a popular audience in the less-precise language of English – see below for examples – the same economists slip into using an incorrect definition of loss aversion.
Conclusion
Behavioral economics has not developed a brilliant newfound qualitative insight that people hate losses more than they like gains. This has been standard in price theory since Alfred Marshall's 1890 Principles of Economics.
References