basilh@virginia.edu
@basilhalperin
Joint with Trevor Chow and J. Zachary Mazlish. Also posted at the EA Forum. November 2023 update: This post is now an academic paper, here, with some different emphasis and some new empirical evidence
In this post, we point out that short AI timelines would cause real interest rates to be high, and would do so under expectations of either unaligned or aligned AI. However, 30- to 50-year real interest rates are low. We argue that this suggests one of two possibilities:
In the rest of this post we flesh out this argument.
An order-of-magnitude estimate is that, if markets are getting this wrong, then there is easily $1 trillion lying on the table in the US treasury bond market alone – setting aside the enormous implications for every other asset class.
Interpretation. We view our argument as the best existing outside view evidence on AI timelines – but also as only one model among a mixture of models that you should consider when thinking about AI timelines. The logic here is a simple implication of a few basic concepts in orthodox economic theory and some supporting empirical evidence, which is important because the unprecedented nature of transformative AI makes “reference class”-based outside views difficult to construct. This outside view approach contrasts with, and complements, an inside view approach, which attempts to build a detailed structural model of the world to forecast timelines (e.g. Cotra 2020; see also Nostalgebraist 2022).
Outline. If you want a short version of the argument, sections I and II (700 words) are the heart of the post. Additionally, the section titles are themselves summaries, and we use text formatting to highlight key ideas.
Real interest rates reflect, among other things:
This claim is compactly summarized in the “Ramsey rule” (and the only math that we will introduce in this post), a version of the “Euler equation” that in one form or another lies at the heart of every theory and model of dynamic macroeconomics:
r = ρ + σg
where:
(Internalizing the meaning of these Greek letters is wholly not necessary.)
While more elaborate macroeconomic theories vary this equation in interesting and important ways, it is common to all of these theories that the real interest rate is higher when either (1) the time discount rate is high or (2) future growth is expected to be high.
We now provide some intuition for these claims.
Time discounting and mortality risk. Time discounting refers to how much people discount the future relative to the present, which captures both (i) intrinsic preference for the present relative to the future and (ii) the probability of death.
The intuition for why the probability of death raises the real rate is the following. Suppose we expect with high probability that humanity will go extinct next year. Then there is no reason to save today: no one will be around to use the savings. This pushes up the real interest rate, since there is less money available for lending.
Economic growth. To understand why higher economic growth raises the real interest rate, the intuition is similar. If we expect to be wildly rich next year, then there is also no reason to save today: we are going to be tremendously rich, so we might as well use our money today while we’re still comparatively poor.
(For the formal math of the Euler equation, Baker, Delong, and Krugman 2005 is a useful reference. The core intuition is that either mortality risk or the prospect of utopian abundance reduces the supply of savings, due to consumption smoothing logic, which pushes up real interest rates.)
Transformative AI and real rates. Transformative AI would either raise the risk of extinction (if unaligned), or raise economic growth rates (if aligned).
Therefore, based on the economic logic above, the prospect of transformative AI – unaligned or aligned – will result in high real interest rates. This is the key claim of this post.
As an example in the aligned case, Davidson (2021) usefully defines AI-induced “explosive growth” as an increase in growth rates to at least 30% annually. Under a baseline calibration where σ=1 and ρ=0.01, and importantly assuming growth rates are known with certainty, the Euler equation implies that moving from 2% growth to 30% growth would raise real rates from 3% to 31%!
For comparison, real rates in the data we discuss below have never gone above 5%.
(In using terms like “transformative AI” or “advanced AI”, we refer to the cluster of concepts discussed in Yudkowsky 2008, Bostrom 2014, Cotra 2020, Carlsmith 2021, Davidson 2021, Karnofsky 2022, and related literature: AI technology that precipitates a transition comparable to the agricultural or industrial revolutions.)
The US 30-year real interest rate ended 2022 at 1.6%. Over the full year it averaged 0.7%, and as recently as March was below zero. Looking at a shorter time horizon, the US 10-year real interest rate is 1.6%, and similarly was below negative one percent as recently as March.
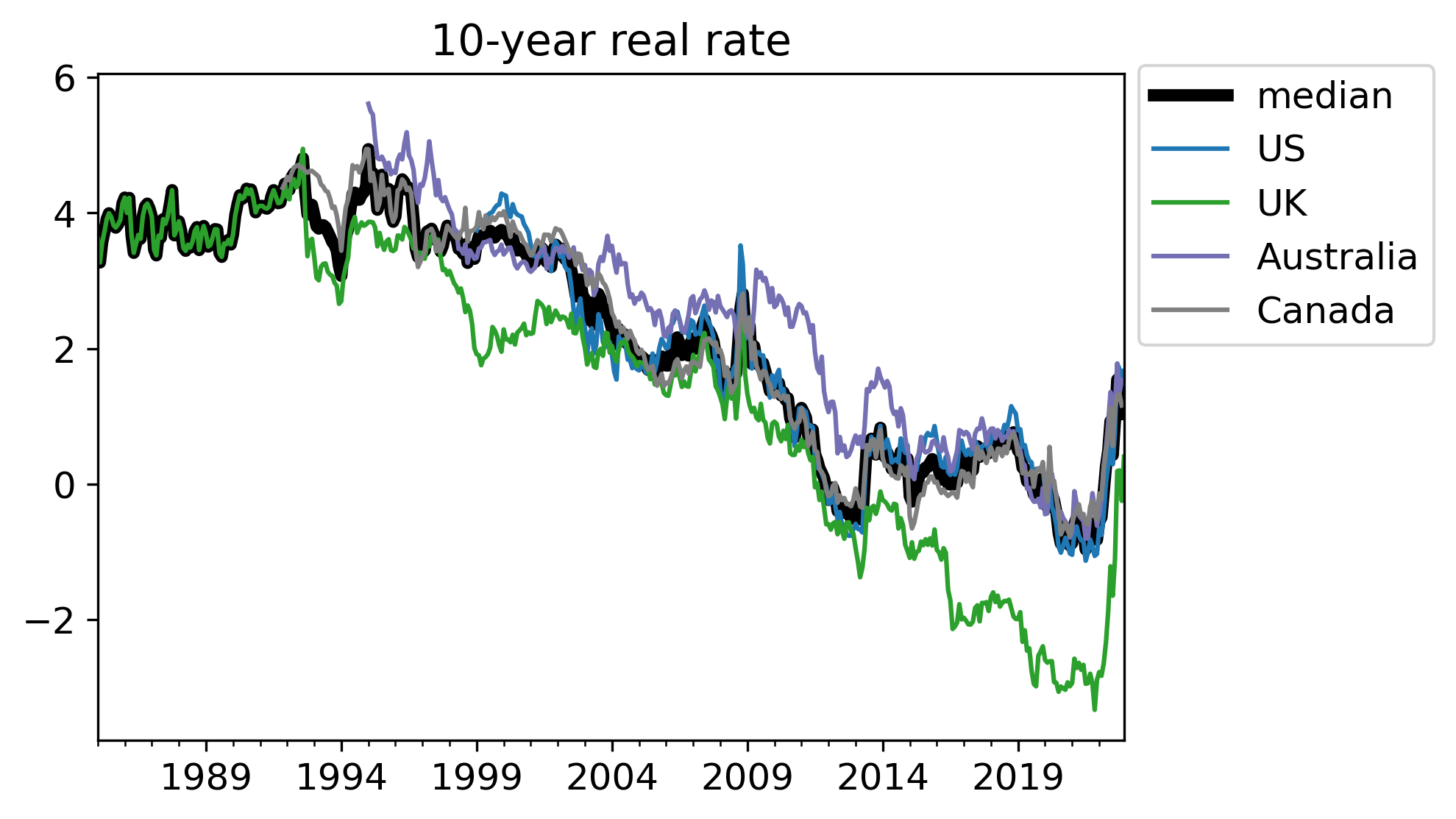
(Data sources used here are explained in section V.)
The UK in autumn 2021 sold a 50-year real bond with a -2.4% rate at the time. Real rates on analogous bonds in other developed countries in recent years have been similarly low/negative for the longest horizons available. Austria has a 100-year nominal bond – being nominal should make its rate higher due to expected inflation – with yields less than 3%.
Thus the conclusion previewed above: financial markets, as evidenced by real interest rates, are not expecting a high probability of either AI-induced growth acceleration or elevated existential risk, on at least a 30-50 year time horizon.
In this section we briefly consider some potentially important complications.
Uncertainty. The Euler equation and the intuition described above assumed certainty about AI timelines, but taking into account uncertainty does not change the core logic. With uncertainty about the future economic growth rate, then the real interest rate reflects the expected future economic growth rate, where importantly the expectation is taken over the risk-neutral measure: in brief, probabilities of different states are reweighted by their marginal utility. We return to this in our quantitative model below.
Takeoff speeds. Nothing in the logic above relating growth to real rates depends on slow vs. fast takeoff speed; the argument can be reread under either assumption and nothing changes. Likewise, when considering the case of aligned AI, rates should be elevated whether economic growth starts to rise more rapidly before advanced AI is developed or only does so afterwards. What matters is that GDP – or really, consumption – ends up high within the time horizon under consideration. As long as future consumption will be high within the time horizon, then there is less motive to save today (“consumption smoothing”), pushing up the real rate.
Inequality. The logic above assumed that the development of transformative AI affects everyone equally. This is a reasonable assumption in the case of unaligned AI, where it is thought that all of humanity will be evaporated. However, when considering aligned AI, it may be thought that only some will benefit, and therefore real interest rates will not move much: if only an elite Silicon Valley minority is expected to have utopian wealth next year, then everyone else may very well still choose to save today.
It is indeed the case that inequality in expected gains from transformative AI would dampen the impact on real rates, but this argument should not be overrated. First, asset prices can be crudely thought of as reflecting a wealth-weighted average across investors. Even if only an elite minority becomes fabulously wealthy, it is their desire for consumption smoothing which will end up dominating the determination of the real rate. Second, truly transformative AI leading to 30%+ economy-wide growth (“Moore’s law for everything”) would not be possible without having economy-wide benefits.
Stocks. One naive objection to the argument here would be the claim that real interest rates sound like an odd, arbitrary asset price to consider; certainly stock prices are the asset price that receive the most media attention.
In appendix 1, we explain that the level of the real interest rate affects every asset price: stocks for instance reflect the present discounted value of future dividends; and real interest rates determine the discount rate used to discount those future dividends. Thus, if real interest rates are ‘wrong’, every asset price is wrong. If real interest rates are wrong, a lot of money is on the table, a point to which we return in section X.
We also argue that stock prices in particular are not a useful indicator of market expectations of AI timelines. Above all, high stock prices of chipmakers or companies like Alphabet (parent of DeepMind) could only reflect expectations for aligned AI and could not be informative of the risk of unaligned AI. Additionally, as we explain further in the appendix, aligned AI could even lower equity prices, by pushing up discount rates.
In section I, we gave theoretical intuition for why higher expected growth or higher existential risk would result in higher interest rates: expectations for such high growth or mortality risk would lead people to want to save less and borrow more today. In this section and the next two, we showcase some simple empirical evidence that the predicted relationships hold in the available data.
Measuring real rates. To compare historical real interest rates to historical growth, we need to measure real interest rates.
Most bonds historically have been nominal, where the yield is not adjusted for changes in inflation. Therefore, the vast majority of research studying real interest rates starts with nominal interest rates, attempts to construct an estimate of expected inflation using some statistical model, and then subtracts this estimate of expected inflation from the nominal rate to get an estimated real interest rate. However, constructing measures of inflation expectations is extremely difficult, and as a result most papers in this literature are not very informative.
Additionally, most bonds historically have had some risk of default. Adjusting for this default premium is also extremely difficult, which in particular complicates analysis of long-run interest rate trends.
The difficulty in measuring real rates is one of the main causes, in our view, of Tyler Cowen’s Third Law: “all propositions about real interest rates are wrong”. Throughout this piece, we are badly violating this (Godelian) Third Law. In appendix 2, we expand on our argument that the source of Tyler’s Third Law is measurement issues in the extant literature, together with some separate, frequent conceptual errors.
Our approach. We take a more direct approach.
Real rates. For our primary analysis, we instead use market real interest rates from inflation-linked bonds. Because we use interest rates directly from inflation-linked bonds – instead of constructing shoddy estimates of inflation expectations to use with nominal interest rates – this approach avoids the measurement issue just discussed (and, we argue, allows us to escape Cowen’s Third Law).
To our knowledge, prior literature has not used real rates from inflation-linked bonds only because these bonds are comparatively new. Using inflation-linked bonds confines our sample to the last ∼20 years in the US, the last ∼30 in the UK/Australia/Canada. Before that, inflation-linked bonds didn’t exist. Other countries have data for even fewer years and less liquid bond markets.
(The yields on inflation-linked bonds are not perfect measures of real rates, because of risk premia, liquidity issues, and some subtle issues with the way these securities are structured. You can build a model and attempt to strip out these issues; here, we will just use the raw rates. If you prefer to think of these empirics as “are inflation-linked bond yields predictive of future real growth” rather than “are real rates predictive of future real growth”, that interpretation is still sufficient for the logic of this post.)
Nominal rates. Because there are only 20 or 30 years of data on real interest rates from inflation-linked bonds, we supplement our data by also considering unadjusted nominal interest rates. Nominal interest rates reflect real interest rates plus inflation expectations, so it is not appropriate to compare nominal interest rates to real GDP growth.
Instead, analogously to comparing real interest rates to real GDP growth, we compare nominal interest rates to nominal GDP growth. The latter is not an ideal comparison under economic theory – and inflation variability could swamp real growth variability – but we argue that this approach is simple and transparent.
Looking at nominal rates allows us to have a very large sample of countries for many decades: we use OECD data on nominal rates available for up to 70 years across 39 countries.
The goal of this section is to show that real interest rates have correlated with future real economic growth, and secondarily, that nominal interest rates have correlated with future nominal economic growth. We also briefly discuss the state of empirical evidence on the correlation between real rates and existential risk.
Real rates vs. real growth. A first cut at the data suggests that, indeed, higher real rates today predict higher real growth in the future:
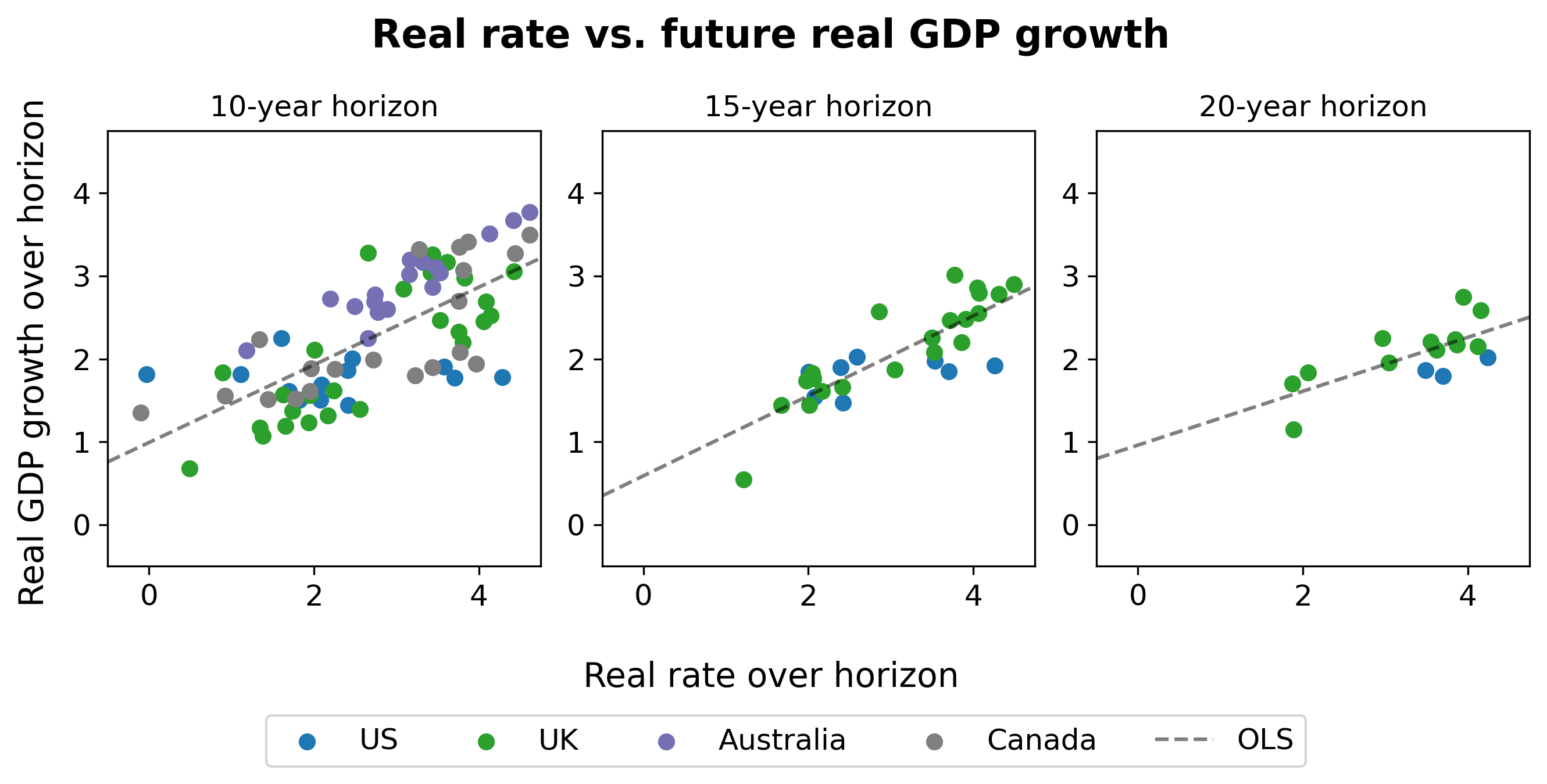
To see how to read these graphs, take the left-most graph (“10-year horizon”) for example. The x-axis shows the level of the real interest rate, as reflected on 10-year inflation linked bonds. The y-axis shows average real GDP growth over the following 10 years.
The middle and right hand graphs show the same, at the 15-year and 20-year horizons. The scatter plot shows all available data for the US (since 1999), the UK (since 1985), Australia (since 1995), and Canada (since 1991). (Data for Australia and Canada is only available at the 10-year horizon, and comes from Augur Labs.)
Eyeballing the figure, there appears to be a strong relationship between real interest rates today and future economic growth over the next 10-20 years.
To our knowledge, this simple stylized fact is novel.
Caveats. “Eyeballing it” is not a formal econometric method; but, this is a blog post not a journal article (TIABPNAJA). We do not perform any formal statistical tests here, but we do want to acknowledge some important statistical points and other caveats.
First, the data points in the scatter plot are not statistically independent: real rates and growth are both persistent variables; the data points contain overlapping periods; and growth rates in these four countries are correlated. These issues are evident even from eyeballing the time series. Second, of course this relationship is not causally identified: we do not have exogenous variation in real growth rates. (If you have ideas for identifying the causal effect of higher real growth expectations on real rates, we would love to discuss with you.)
Relatedly, many other things are changing in the world which are likely to affect real rates. Population growth is slowing, retirement is lengthening, the population is aging. But under AI-driven “explosive” growth – again say 30%+ annual growth, following the excellent analysis of Davidson (2021) – then, we might reasonably expect that this massive of an increase in the growth rate would drown out the impact of any other factors.
Nominal rates vs. nominal growth. Turning now to evidence from nominal interest rates, recall that the usefulness of this exercise is that while there only exists 20 or 30 years of data on real interest rates for two countries, there is much more data on nominal interest rates.
We simply take all available data on 10-year nominal rates from the set of 39 OECD countries since 1954. The following scatterplot compares the 10-year nominal interest versus nominal GDP growth over the succeeding ten years by country:
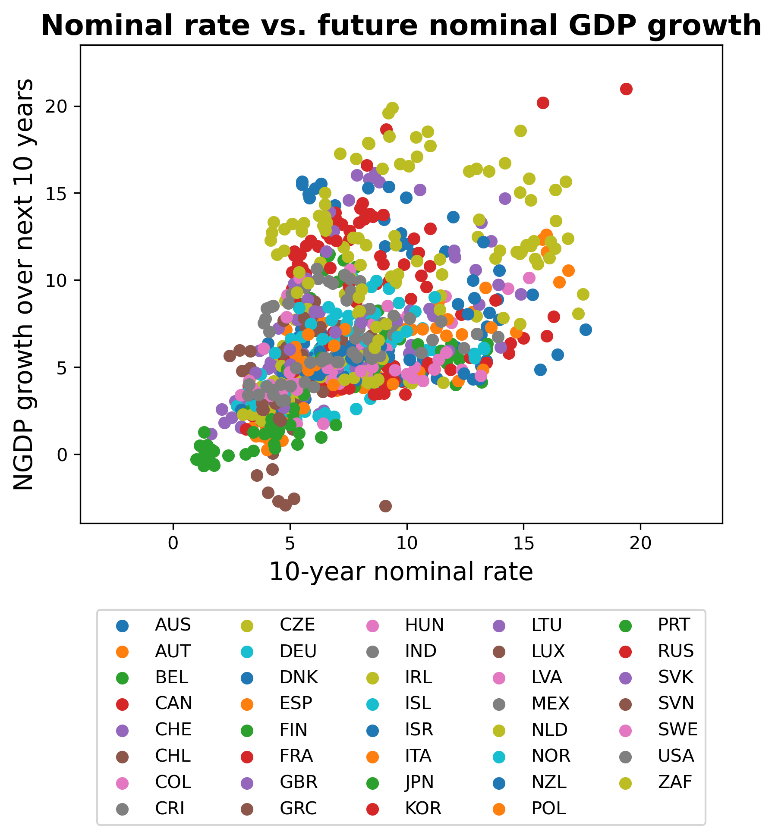
Again, there is a strong positive – if certainly not perfect – relationship. (For example, the outlier brown dots at the bottom of the graph are Greece, whose high interest rates despite negative NGDP growth reflect high default risk during an economic depression.)
The same set of nontrivial caveats apply to this analysis as above.
We consider this data from nominal rates to be significantly weaker evidence than the evidence from real rates, but corroboration nonetheless.
Backing out market-implied timelines. Taking the univariate pooled OLS results from the real rate data far too seriously, the fact that the 10-year real rate in the US ended 2022 at 1.6% would predict average annual real GDP growth of 2.6% over the next 10 years in the US; the analogous interest rate of -0.2% in the UK would predict 0.7% annual growth over the next 10 years in the UK. Such growth rates, clearly, are not compatible with the arrival of transformative aligned AI within this horizon.
We have argued that in the theory, real rates should be higher in the face of high economic growth or high mortality risk; empirically, so far, we have only shown a relationship between real rates and growth, but not between real rates and mortality.
Showing that real rates accurately reflect changes in existential risk is very difficult, because there is no word-of-god measurement of how existential risk has evolved over time.
We would be very interested in pursuing new empirical research examining “asset pricing under existential risk”. In appendix 3, we perform a scorched-earth literature review and find essentially zero existing empirical evidence on real rates and existential risks.
Disaster risk. In particular, the extant literature does not study existential risks but instead “merely” disaster risks, under which real assets are devastated but humanity is not exterminated. Disaster risks do not necessarily raise real rates – indeed, such risks are thought to lower real rates due to precautionary savings. That notwithstanding, some highlights of the appendix review include a small set of papers finding that individuals with a higher perceived risk of nuclear conflict during the Cold War saved less, as well as a paper noting that equities which were headquartered in cities more likely to be targeted by Soviet missiles did worse during the Cuban missile crisis (see also). Our assessment is that these and the other available papers on disaster risks discussed in the appendix have severe limitations for the purposes here.
Individual mortality risk. We judge that the best evidence on this topic comes instead from examining the relationship between individual mortality risk and savings/investment behavior. The logic we provided was that if humanity will be extinct next year, then there is no reason to save, pushing up the real rate. Similar logic says that at the individual level, a higher risk of death for any reason should lead to lower savings and less investment in human capital. Examples of lower savings at the individual level need not raise interest rates at the economy-wide level, but do provide evidence for the mechanism whereby extinction risk should lead to lower saving and thus higher interest rates.
One example comes from Malawi, where the provision of a new AIDS therapy caused a significant increase in life expectancy. Using spatial and temporal variation in where and when these therapeutics were rolled out, it was found that increased life expectancy results in more savings and more human capital investment in the form of education spending. Another experiment in Malawi provided information to correct pessimistic priors about life expectancy, and found that higher life expectancy directly caused more investment in agriculture and livestock.
A third example comes from testing for Huntington’s disease, a disease which causes a meaningful drop in life expectancy to around 60 years. Using variation in when people are diagnosed with Huntington’s, it has been found that those who learn they carry the gene for Huntington’s earlier are 30 percentage points less likely to finish college, which is a significant fall in their human capital investment.
Studying the effect on savings and real rates from increased life expectancy at the population level is potentially intractable, but would be interesting to consider further. Again, in our assessment, the best empirical evidence available right now comes from the research on individual “existential” risks and suggests that real rates should increase with existential risk.
Section VI used historical data to go from the current real rate to a very crude market-implied forecast of growth rates; in this section, we instead use a model to go from existing forecasts of AI timelines to timeline-implied real rates. We aim to show that under short AI timelines, real interest rates would be unrealistically elevated.
This is a useful exercise for three reasons. First, the historical data is only able to speak to growth forecasts, and therefore only able to provide a forecast under the possibly incorrect assumption of aligned AI. Second, the empirical forecast assumes a linear relationship between the real rate and growth, which may not be reasonable for a massive change caused by transformative AI. Third and quite important, the historical data cannot transparently tell us anything about uncertainty and the market’s beliefs about the full probability distribution of AI timelines.
We use the canonical (and nonlinear) version of the Euler equation – the model discussed in section I – but now allow for uncertainty on both how soon transformative AI will be developed and whether or not it will be aligned. The model takes as its key inputs (1) a probability of transformative AI each year, and (2) a probability that such technology is aligned.
The model is a simple application of the stochastic Euler equation under an isoelastic utility function. We use the following as a baseline, before considering alternative probabilities:
Thus, to summarize: by default, GDP grows at 1.8% per year. Every year, there is some probability (based on Cotra) that transformative AI is developed. If it is developed, there is a 15% probability the world ends, and an 85% chance GDP growth jumps to 30% per year.
We have built a spreadsheet here that allows you to tinker with the numbers yourself, such as adjusting the growth rate under aligned AI, to see what your timelines and probability of alignment would imply for the real interest rate. (It also contains the full Euler equation formula generating the results, for those who want the mathematical details.) We first estimate real rates under the baseline calibration above, before considering variations in the critical inputs.
Baseline results. The model predicts that under zero probability of transformative AI, the real rate at any horizon would be 2.8%. In comparison, under the baseline calibration just described based on Cotra timelines, the real rate at a 30-year horizon would be pushed up to 5.9% – roughly three percentage points higher.
For comparison, the 30-year real rate in the US is currently 1.6%.
While the simple Euler equation somewhat overpredicts the level of the real interest rate even under zero probability of transformative AI – the 2.8% in the model versus the 1.6% in the data – this overprediction is explainable by the radical simplicity of the model that we use and is a known issue in the literature. Adding other factors (e.g. precautionary savings) to the model would lower the level. Changing the level does not change its directional predictions, which help quantitatively explain the fall in real rates over the past ∼30 years.
Therefore, what is most informative is the three percentage point difference between the real rate under Cotra timelines (5.9%) versus under no prospect of transformative AI (2.8%): Cotra timelines imply real interest rates substantially higher than their current levels.
Now, from this baseline estimate, we can also consider varying the key inputs.
Varying assumptions on P(misaligned|AGI). First consider changing the assumption that advanced AI is 15% likely to be unaligned (conditional on the development of AGI). Varying this parameter does not have a large impact: moving from 0% to 100% probability of misalignment raises the model’s predicted real rate from 5.8% only to 6.3%.
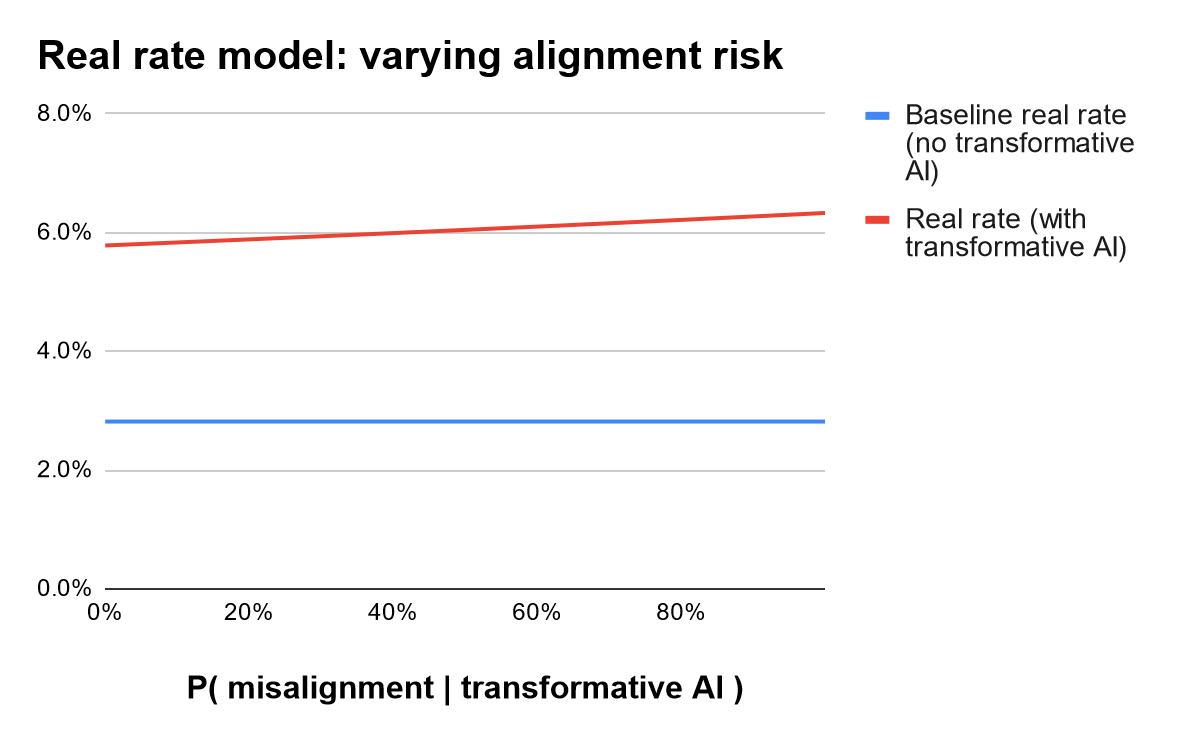
Varying assumptions on timelines. Second, consider making timelines shorter or longer. In particular, consider varying the probability of development by 2043, which we use as a benchmark per the FTX Future Fund.
We scale the Cotra timelines up and down to vary the probability of development by 2043. (Specifically: we target a specific cumulative probability of development by 2043; and, following Cotra, if the annual probability up until 2030 is x, then it is 1.5x in the subsequent seven years up through 2036, and it is 2x in the remaining years of the 30-year window.)
As the next figure shows and as one might expect, shorter AI timelines have a very large impact on the model’s estimate for the real rate.
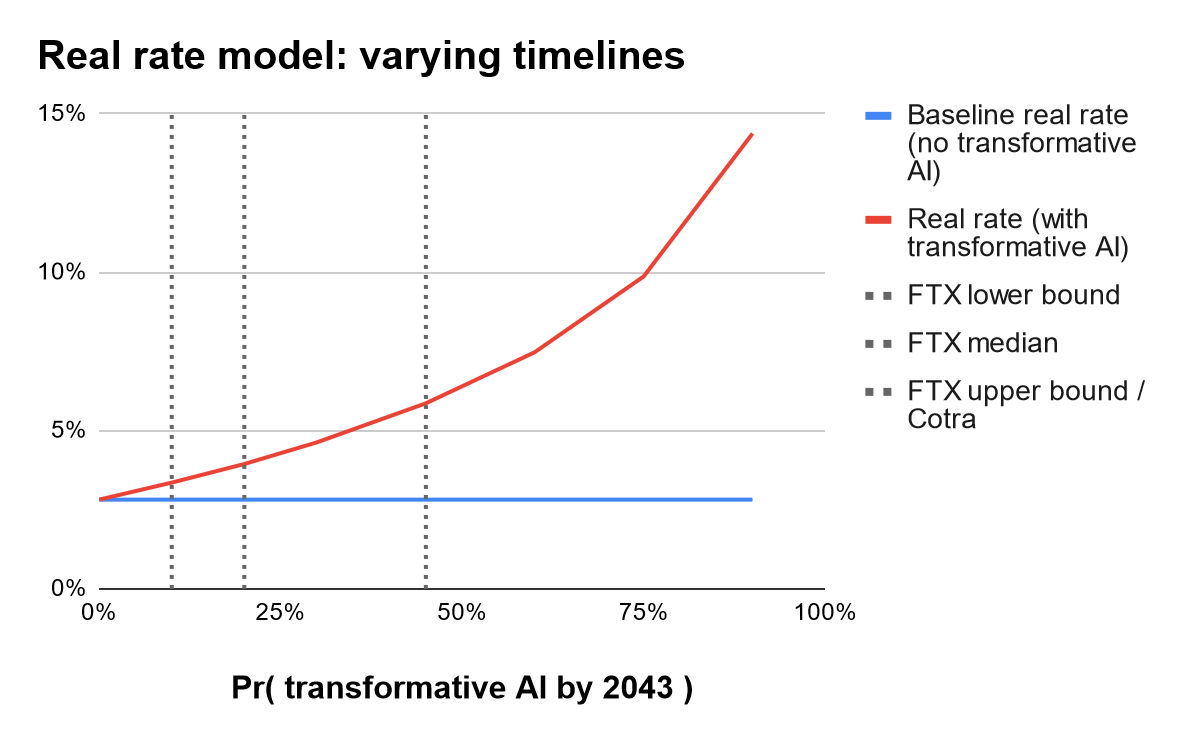
These results strongly suggest that any timeline shorter than or equal to the Cotra timeline is not being expected by financial markets.
While it is not possible to back out exact numbers for the market’s implicit forecast for AI timelines, it is reasonable to say that the market is decisively rejecting – i.e., putting very low probability on – the development of transformative AI in the very near term, say within the next ten years.
Consider the following examples of extremely short timelines:
Real rate movements of these magnitudes are wildly counterfactual. As previously noted, real rates in the data used above have never gone above even 5%.
Stagnation. As a robustness check, in the configurable spreadsheet we allow you to place some yearly probability on the economy stagnating and growing at 0% per year from thereon. Even with a 20% chance of stagnation by 2053 (higher than realistic), under Cotra timelines, the model generates a 2.1% increase in 30-year rates.
Recent market movements. Real rates have increased around two percentage points since the start of 2022, with the 30-year real rate moving from -0.4% to 1.6%, approximately the pre-covid level. This is a large enough move to merit discussion. While this rise in long-term real rates could reflect changing market expectations for timelines, it seems much more plausible that high inflation, the Russia-Ukraine war, and monetary policy tightening have together worked to drive up short-term real rates and the risk premium on long-term real rates.
Should we update on the fact that markets are not expecting very short timelines?
Probably!
As a prior, we think that market efficiency is reasonable. We do not try to provide a full defense of the efficient markets hypothesis (EMH) in this piece given that it has been debated ad nauseum elsewhere, but here is a scaffolding of what such an argument would look like.
Loosely, the EMH says that the current price of any security incorporates all public information about it, and as such, you should not expect to systematically make money by trading securities.
This is simply a no-arbitrage condition, and certainly no more radical than supply and demand: if something is over- or under-priced, you’ll take action based on that belief until you no longer believe it. In other words, you’ll buy and sell it until you think the price is right. Otherwise, there would be an unexploited opportunity for profit that was being left on the table, and there are no free lunches when the market is in equilibrium.
As a corollary, the current price of a security should be the best available risk-adjusted predictor of its future price. Notice we didn’t say that the price is equal to the “correct” fundamental value. In fact, the current price is almost certainly wrong. What we did say is that it is the best guess, i.e. no one knows if it should be higher or lower.
Testing this hypothesis is difficult, in the same way that testing any equilibrium condition is difficult. Not only is the equilibrium always changing, there is also a joint hypothesis problem which Fama (1970) outlined: comparing actual asset prices to “correct” theoretical asset prices means you are simultaneously testing whatever asset pricing model you choose, alongside the EMH.
In this sense, it makes no sense to talk about “testing” the EMH. Rather, the question is how quickly prices converge to the limit of market efficiency. In other words, how fast is information diffusion? Our position is that for most things, this is pretty fast!
Here are a few heuristics that support our position:
Remember: if real interest rates are wrong, all financial assets are mispriced. If real interest rates “should” rise three percentage points or more, that is easily hundreds of billions of dollars worth of revaluations. It is unlikely that sharp market participants are leaving billions of dollars on the table.
While our prior in favor of efficiency is fairly strong, the market could be currently failing to anticipate transformative AI, due to various limits to arbitrage.
However, if you do believe the market is currently wrong about the probability of short timelines, then we now argue there are two courses of action you should consider taking:
Under the logic argued above, if you genuinely believe that AI timelines are short, then you should consider putting your money where your mouth is: bet that real rates will rise when the market updates, and potentially earn a lot of money if markets correct. Shorting (or going underweight) government debt is the simplest way of expressing this view.
Indeed, AI safety researcher Paul Christiano has written publicly that he is (or was) short 30-year government bonds.
If short timelines are your true belief in your heart of hearts, and not merely a belief in a belief, then you should seriously consider how much money you could earn here and what you could do with those resources.
Implementing the trade. For retail investors, betting against treasuries via ETFs is perhaps simplest. Such trades can be done easily with retail brokers, like Schwab.
(i) For example, one could simply short the LTPZ ETF, which holds long-term real US government debt (effective duration: 20 years).
(ii) Alternatively, if you would prefer to avoid engaging in shorting yourself, there are ETFs which will do the shorting for you, with nominal bonds: TBF is an ETF which is short 20+ year treasuries (duration: 18 years); TBT is the same, but levered 2x; and TTT is the same, but levered 3x. There are a number of other similar options. Because these ETFs do the shorting for you, all you need to do is purchase shares of the ETFs.
Back of the envelope estimate. A rough estimate of how much money is on the table, just from shorting the US treasury bond market alone, suggests there is easily $1 trillion in value at stake from betting that rates will rise.
Alternatively, returning to the LTPZ ETF with its duration of 20 years, a 3 percentage point rise in rates would cause its value to fall by 60%. Using the 3x levered TTT with duration of 18 years, a 3 percentage point rise in rates would imply a mouth-watering cumulative return of 162%.
While fully fleshing out the trade analysis is beyond the scope of this post, this illustration gives an idea of how large the possibilities are.
The alternative to this order-of-magnitude estimate would be to build a complete bond pricing model to estimate more precisely the expected returns of shorting treasuries. This would need to take into account e.g. the convexity of price changes with interest rate movements, the varied maturities of outstanding bonds, and the different varieties of instruments issued by the Treasury. Further refinements would include trading derivatives (e.g. interest rate futures) instead of shorting bonds directly, for capital efficiency, and using leverage to increase expected returns.
Additionally, the analysis could be extended beyond the US government debt market, again since changes to real interest rates would plausibly impact the price of every asset: stocks, commodities, real estate, everything.
(If you would be interested in fully scoping out possible trades, we would be interested in talking.)
Trade risk and foom risk. We want to be clear that – unless you are risk neutral, or can borrow without penalty at the risk-free rate, or believe in short timelines with 100% probability – then such a bet would not be a free lunch: this is not an “arbitrage” in the technical sense of a risk-free profit. One risk is that the market moves in the other direction in the short term, before correcting, and that you are unable to roll over your position for liquidity reasons.
The other risk that could motivate not making this bet is the risk that the market – for some unspecified reason – never has a chance to correct, because (1) transformative AI ends up unaligned and (2) humanity’s conversion into paperclips occurs overnight. This would prevent the market from ever “waking up”.
However, to be clear, expecting this specific scenario requires both:
You should be sure that your beliefs are actually congruent with these requirements, if you want to refuse to bet that real rates will rise. Additionally, we will see that the second suggestion in this section (“impatient philanthropy”) is not affected by the possibility of foom scenarios.
If prevailing interest rates are lower than your subjective discount rate – which is the case if you think markets are underestimating prospects for transformative AI – then simple cost-benefit analysis says you should save less or even borrow today.
An illustrative example. As an extreme example to illustrate this argument, imagine that you think that there is a 50% chance that humanity will be extinct next year, and otherwise with certainty you will have the same income next year as you do this year. Suppose the market real interest rate is 0%. That means that if you borrow $10 today, then in expectation you only need to pay $5 off, since 50% of the time you expect to be dead.
It is only if the market real rate is 100% – so that your $10 loan requires paying back $20 next year, or exactly $10 in expectation – that you are indifferent about borrowing. If the market real rate is less than 100%, then you want to borrow. If interest rates are “too low” from your perspective, then on the margin this should encourage you to borrow, or at least save less.
Note that this logic is not affected by whether or not the market will “correct” and real rates will rise before everyone dies, unlike the logic above for trading.
Borrowing to fund philanthropy today. While you may want to borrow today simply to fund wild parties, a natural alternative is: borrow today, locking in “too low” interest rates, in order to fund philanthropy today. For example: to fund AI safety work.
We can call this strategy “impatient philanthropy”, in analogy to the concept of “patient philanthropy”.
This is not a call for philanthropists to radically rethink their cost-benefit analyses. Instead, we merely point out: ensure that your financial planning properly accounts for any difference between your discount rate and the market real rate at which you can borrow. You should not be using the market real rate to do your financial planning. If you have a higher effective discount rate due to your AI timelines, that could imply that you should be borrowing today to fund philanthropic work.
Relationship to impatient philanthropy. The logic here has a similar flavor to Phil Trammell’s “patient philanthropy” argument (Trammell 2021) – but with a sign flipped. Longtermist philanthropists with a zero discount rate, who live in a world with a positive real interest rate, should be willing to save all of their resources for a long time to earn that interest, rather than spending those resources today on philanthropic projects. Short-timeliners have a higher discount rate than the market, and therefore should be impatient philanthropists.
(The point here is not an exact analog to Trammell 2021, because the paper there considers strategic game theoretic considerations and also takes the real rate as exogenous; here, the considerations are not strategic and the endogeneity of the real rate is the critical point.)
We do not claim to have special technical insight into forecasting the likely timeline for the development of transformative artificial intelligence: we do not present an inside view on AI timelines.
However, we do think that market efficiency provides a powerful outside view for forecasting AI timelines and for making financial decisions. Based on prevailing real interest rates, the market seems to be strongly rejecting timelines of less than ten years, and does not seem to be placing particularly high odds on the development of transformative AI even 30-50 years from now.
We argue that market efficiency is a reasonable benchmark, and consequently, this forecast serves as a useful prior for AI timelines. If markets are wrong, on the other hand, then there is an enormous amount of money on the table from betting that real interest rates will rise. In either case, this market-based approach offers a useful framework: either for forecasting timelines, or for asset allocation.
Opportunities for future work. We could have put 1000 more hours into the empirical side or the model, but, TIABPNAJA. Future work we would be interested in collaborating on or seeing includes:
Thanks especially to Leopold Aschenbrenner, Nathan Barnard, Jackson Barkstrom, Joel Becker, Daniele Caratelli, James Chartouni, Tamay Besiroglu, Joel Flynn, James Howe, Chris Hyland, Stephen Malina, Peter McLaughlin, Jackson Mejia, Laura Nicolae, Sam Lazarus, Elliot Lehrer, Jett Pettus, Pradyumna Prasad, Tejas Subramaniam, Karthik Tadepalli, Phil Trammell, and participants at ETGP 2022 for very useful conversations on this topic and/or feedback on drafts.
Update: we have now posted a comment summarising our responses to the feedback we have received so far.
OpenAI’s ChatGPT model on what will happen to real rates if transformative AI is developed:

Some framings you can use to interpret this post: